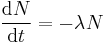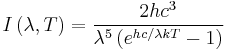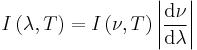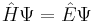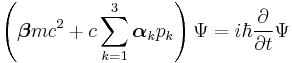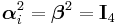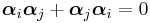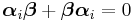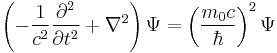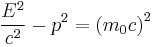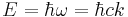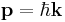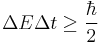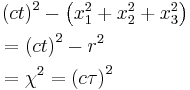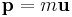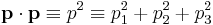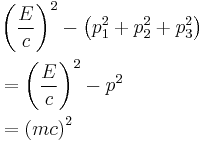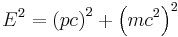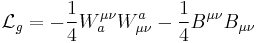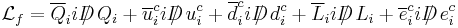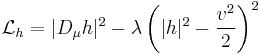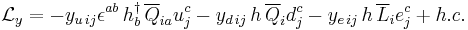Mathematical descriptions of physical laws
Physical laws are often summarized by a single equation, or at least a small set of equations. This article tabulates many of the important bands of physics where such laws occur.
Contents |
General principles
Conservation and continuity
All conserved quantities can be written as a conservation law (also as continuity equation). The formalism of how conservation laws can be used is given below. See also Noether's theorem.
| Let | so that |
| S = Closed surface of region to calculate flux, arbitrary but fixed for calculation, R = Region of space bounded by S containing total amount of quantity Q, which occupies the closed system, r = position vector, q = any conserved quantity as a function of space and time within the closed system (since it may flow throughout, but the total amount in the system is still constant and independent of space and time), I = current of q, N = number of discrete constituents of the system, e.g. particles possessing momenta |
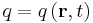
|
Then we have the following equations.
Summary of conservative formalisms
The following appear trivial and self-evident, but often calculations for conservative situations are applied in one of these forms.
| Equation type | Discrete equation | Continuum equation |
|---|---|---|
| Constancy equation | All changes
|
Differential changes
|
| System equation/s | 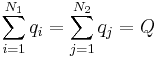 |
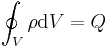 |
| Time derivatives,
Current |
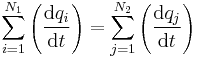
|
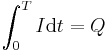 |
| Time–area derivatives,
Current density, flux |
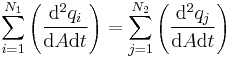
|
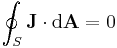
by the divergence theorem;
|
Summary of classical continuity equations
The general continuity equation can be written in differential or integral form:
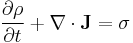
|
In the table below, the fluxes, flows and continuity equations have been collected for comparison. Also alternative forms using currents have been included; often these forms are used in introductory transport mechanics since they are simply statements which relate current and flux, simply by conservation of the quantity as it flows. The nomenclature is very similar throughout the equations, to make clear the nature of transport much of the nomenclature been re-stated.
| Phyics, conserved quantity | Conserved quantity q | Volume density ρ (of q) | Flux J (of q) | Vector DE | Conservative equation |
|---|---|---|---|---|---|
| Hydrodynamics, fluid |
m = mass (kg) | ρ = volume mass density (kg m-3) | ρ u, where u = velocity field of fluid (m s-1) |
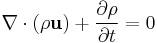 |
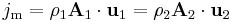
jm = mass current at the cross-section (kg s-1) |
| Electromagnetism, electric charge | q = electric charge (C) | ρ = volume electric charge density (C m-3) | J = electric current density (A m-2) | 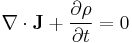 |
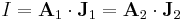
I = electric current at the cross-section (A) |
| Thermodynamics, energy | E = energy (J) | u = volume energy density (J m-3) | q = heat flux (W m-2) | 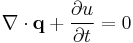 |
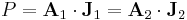
P = thermal current at the cross-section (W) |
| Quantum mechanics, probability | p = Pr(x,t) = probability distribution | P = P(x,t) = probability density function (m-3) | j = probability current/flux | 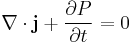 |
Principle of least action
A system always minimizes the action associated with all parts of the system. Various minimized action formulations are given, all of course equivalent.
| Formulation | Nomenclature | Equations |
|---|---|---|
| Statement | 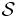 = action = action |
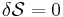 |
| Maupertuis'-Euler | t = time, t1, t2 = initial and final times, |
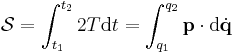
|
| Jacobi's | s = arc length, C = curve, |
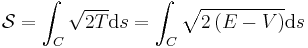
|
| Lagrange | L = Lagrangian | 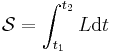
|
Classical mechanics
Galilean frame transforms
For classical (Galileo-Newtonian) mechanics, the transformation law from one inertial or accelerating (including rotation) frame (reference frame travelling at constant velocity - including zero) to another is the Galilean transform.
Unprimed quantities refer to position, velocity and acceleration in one frame F; primed quantities refer to position, velocity and acceleration in another frame F' moving at translational velocity V or angular velocity Ω relative to F. Conversely F moves at velocity (—V or —Ω) relative to F'. The situation is similar for relative accelerations.
| Motion of entities | Inertial frames | Accelerating frames | |
|---|---|---|---|
| Translation
V = Constant relative velocity between two inertial frames F and F'. |
Relative position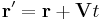 Relative velocity |
Relative accelerations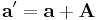 Apparent/ficticous forces |
|
| As measured in frame F: r = position |
As measured in frame F': r' = position |
||
| Rotation
Ω = Constant relative angular velocity between two frames F and F'. |
Relative angular position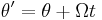 Relative velocity |
Relative accelerations Apparent/ficticous torques |
|
|
As measured in frame F: |
As measured in frame F': r' = angular position |
||
Laws of classical mechanics
The following[1][2] general approaches to classical mechanics are summarized below in the order of establishment. They are equivalent formulations, Newton's is very commonly used due to simplicity, but Hamilton's and Lagrange's equations are more general, and their range can extend into other branches of physics with suitable modifications.
| Laws | Equation |
|---|---|
| Newton's laws | The laws can be summarized by two equations:
For a dynamical system the two equations (effectively) combine into one: |
| p = momentum of body, Fij = force ON body i BY body j, |
|
| Euler-Lagrange equations | Euler-Lagrange equation system
Euler-Lagrange equation |
| qi = generalized coordinates, pi = generalized momenta |
|
| Hamilton's equation system | 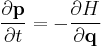 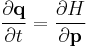
The Hamiltonian as a function of generalized coordinates and momenta has the general form: |
| Appell's equation | 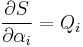
where: |
| Qi = generalized force αi = generalized acceleration |
Laws of thermodynamics
Main laws
| Property/effect | Equation |
|---|---|
| Zeroth law of thermodynamics (systems in thermal equilibrium) | 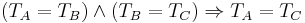 |
| First law of thermodynamics | 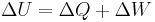
Internal energy increase |
| Second Law of Thermodynamics | 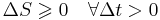 |
| Third Law of Thermodynamics | 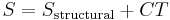 |
Extensions of the laws
| Property or effect | Equation |
|---|---|
| Fundamental thermodynamic relation (systems in thermal equilibrium) | 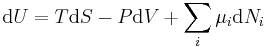 |
| Onsager reciprocal relations | 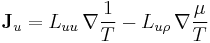
|
| u = Energy Density (J m−3) J = Energy Flux Density (W m−2) |
Maxwell's relations
The potentials as functions of their natural variables are:
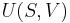 = Internal energy
= Internal energy
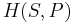 = Enthalpy
= Enthalpy
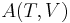 = Helmholtz free energy
= Helmholtz free energy
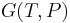 = Gibbs free energy
= Gibbs free energy
|
|
Laws of gravitation
Modern laws
ETF and GEM Equations
Main article: Einstein field equations (ETF), Gravitomagnetism (GEM)
In a relatively flat spacetime due to weak gravitational fields (by General Relativity), the following gravitational analogues of Maxwell's equations can be found, to describe an analogous Gravitomagnetic Field. They are well established by the theory, but have yet to be verified by experiment.[3]
| Laws | Nomenclature | Equations |
|---|---|---|
| Einstein Tensor Field (ETF) Equations | Λ = Cosmological Constant Rμν = Ricci Curvature Tensor |
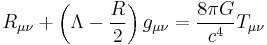
|
| GEM Equations | g = Gravitational Field ξ = Gravitomagnetic Field |
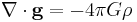
|
| Gravitomagnetic Lorentz Force | Ω = Gravitational Torsion Field | 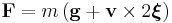
|
Classical laws
It can be found that Kepler's Laws, though originally discovered from planetary observations (also due to Tycho Brahe), are true for any central forces.[4]
For Kepler's 1st law, the equation is nothing physically fundamental; simply the polar equation of an ellipse where the pole (origin of polar coordinate system) is positioned at a focus of the ellipse, centred on the central star.
e = (elliptic) eccentricity
a = elliptic semi-major axes = planet aphelion
b = elliptic semi-minor axes = planet perihelion
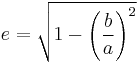
| Property or effect | Equation |
|---|---|
| Newton's law of universal gravitation | 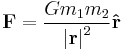
For a non uniform mass distribution this becomes: |
| ρ = Local mass density of body V = Volume of body |
|
| Gauss' law for gravity | 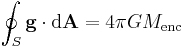 |
| Kepler's 1st Law
Planets move in an ellipse, |
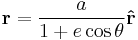 |
| Kepler's 2nd Law | 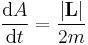 |
| Kepler's 3rd Law | 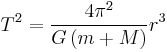 |
Laws of electromagnetism
Maxwell's equations
No Magnetic Monopoles
| Name | Differential form |
|---|---|
| Gauss's law for electrostatics | 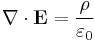 |
| Gauss's law for magnetostatics | 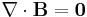 |
| Maxwell–Faraday law (Faraday's law of induction) |
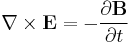 |
| Maxwell-Ampère circuital law (Ampere's Law with Maxwell's correction) |
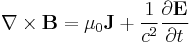 |
| Lorentz force law | 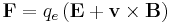 |
Monopoles Inclusion
To introduce monopoles mathematically, magnetic pole strength qm (AKA magnetic charge or monopole charge, all synonymous) is defined, treating magnetic poles analogously to electric charges - see section below. Pole srength can be quantified into volume densities, currents and current densities just like electric charge.
The mathematical convention is: north charge N; qm > 0, south charge S; qm < 0, neutral charge; qm = 0 (equivalent to no net magnetic charge, or none at all).
From the SI system two units are possible, Wb (Weber) and A m (Ampere-metre). Dimensional analysis leads to the conversion:
Maxwell's Equations would become one of the columns in the table below, at least theoretically. Subscripts e are electric charge quantities; subscripts m are magnetic charge quantities. They are consistent if no magnetic monopoles exist, since the monopole quantities are then zero and the equations reduce to the original form of Maxwell's equations.
| Name | Weber (Wb) | Ampere meter (A m) convention |
|---|---|---|
| Gauss's law for electrostatics | 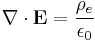 |
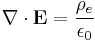 |
| Gauss's law for magnetostatics | 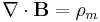 |
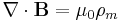 |
| Faraday's law of induction | 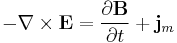 |
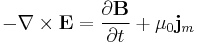 |
| Ampère's law | 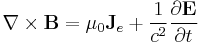 |
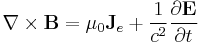 |
| Lorentz force equation | 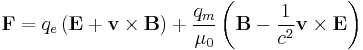 |
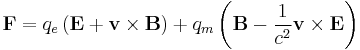 |
Pre-Maxwell laws
These laws are not fundamental, since they can be derived from Maxwell's Equations. Coulomb's Law can be found from Gauss' Law (electrostatic form) and the Biot-Savart Law can be deduced from Ampere's Law (magnetostatic form). Lenz' Law and Faraday's Law can be incorporated into the Maxwell-Faraday equation. Nonetheless they are still very effective for simple calculations.
| Name | Equation |
|---|---|
| Coulomb's Law | 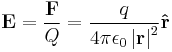 |
| Biot-Savart law | 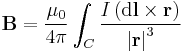 |
| Lenz's law | The magnetic flux set up by the current in a conductor tends to oppose that current. |
| Kirchoff's Laws | emf loop rule around any closed circuit
Current law at junctions |
Parallels between classical gravitation and electromagnetism
Below the mathematics can only be incorporated into magnetism if magnetic monopoles exist. If they do not, then as stated in the above Laws of electromagnetism section the pole strength is zero and monopole quantities disappear.
Let:
α = Mass, electric charge or magnetic monopole strength,
Λ = Gravitational, electric field or magnetic field,
F = Force,
Π = Mass moment, electric dipole due to charges, magnetic moment due to current or monopoles,
d = Pole separation for electric/magnetic dipoles,
r = Position vector,
X = Proportionality constants related to other physical constants,
Y = Physical constant, gravitational constant G, vacuum permittivity ε0, vacuum permeability μ0,
ФΛ = Field flux,
n, m = any from +1, 0, −1
and using the same notation as before in the General principles section above, we have the following.
| Property or effect | Equation |
|---|---|
| Constants | 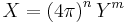 |
| Quantification: volume densities, currents, current densities | 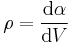
|
| Force due to field | 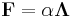
For an array of point masses, charges or poles: where the unit vector rij corresponds to the separation between a pair of point masses charges or poles: |
| Mass moments or electric/magnetic dipole moments | 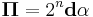 |
| Mass moment density, electric or magnetic dipole moment densities (polarization/ magnetization) | 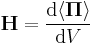
The average moment is simply: |
| Field flux | 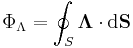 |
| "Gaussian law" | Equivalent forms (by the divergence theorem) are:
|
Radiation laws
Photonics
Subscripts 1 and 2 refer to initial and final optical media respectively.
| Name | Equations |
|---|---|
| Law of reflection | 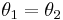 |
| θ = angle of refraction relative to the interface normal | |
| Law of refraction, Snell's law | 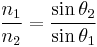 |
| n = refractive index of medium |
|
| Angle of total polarisation |  |
| θB = Reflective polarization angle, Brewster's angle | |
| intensity from polarized light, |
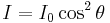 |
| I0 = Initial intensity, I = Transmitted intensity, |
|
| Bragg's law (solid state diffraction) | 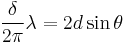 For constructive interference: |
| d = lattice spacing δ = phase differance between two waves |
|
| Huygen-Fresnel-Kirchhoff principle | ![A \mathbf ( \mathbf{r} ) = \frac{-i}{2\lambda} \iint_\mathrm{aperture} \frac{e^{i \mathbf{k} \cdot \left ( \mathbf{r} %2B \mathbf{r}_0 \right ) }}{ \left | \mathbf{r} \right |\left | \mathbf{r}_0 \right |} \left [ \cos \alpha_0 - \cos \alpha \right ] \mathrm{d}S \,\!](/2012-wikipedia_en_all_nopic_01_2012/I/0f572a28f44a6d0ea7e00217c96084ba.png)
where |
| r0 = position from source to aperture, incident on it r = position from aperture diffracted from it to a point |
|
| Kirchhoff's diffraction formula | ![A \left ( \mathbf{r} \right ) = - \frac{1}{4 \pi} \iint_\mathrm{aperture} \frac{e^{i \mathbf{k} \cdot \mathbf{r}_0}}{\left | \mathbf{r}_0 \right |} \left[ i \left | \mathbf{k} \right | U_0 \left ( \mathbf{r}_0 \right ) \cos{\alpha} %2B \frac {\partial A_0 \left ( \mathbf{r}_0 \right )}{\partial n} \right ] \mathrm{d}S](/2012-wikipedia_en_all_nopic_01_2012/I/29a039c7fd090bf8e336d75cc917a2a6.png) |
These ratios are sometimes also used, following simply from other definitions of refractive index, wave phase velocity, and the luminal speed equation:
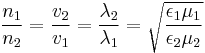
where:
ε = permittivity of medium,
μ = permeability of medium,
λ = wavelength of light in medium,
v = speed of light in media.
Radiation
| Name | Equations |
|---|---|
| Radioactive decay | Statistical decay of a radionuclide:
|
| N = N(t) = Number of atoms at time t t = Time (s) |
|
| Stefan–Boltzmann law | 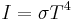 |
| I = Intensity (W m-2) | |
| Wien's displacement law | 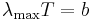 |
| b = Wein constant (m K) | |
| Planck's law | 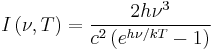
|
| I = Specific radiative intensity (W m–2 Hz–1 sr–1) |
Quantum mechanics
Wavefunction equations
| Name | Equation |
|---|---|
| Schrödinger equation | General classical form for all wavefunctions ψ = ψ(r, t):
|
| Dirac equation | For elementary spin-1/2 particles:
Dirac matrices: |
| Klein–Gordon equation | General form for all relativistic wavefunctions ψ = ψ(r, t):
Can be obtained by inserting the quantum operators into the momentum-energy invariant of relativistic mechanics:
|
Commonly used corollaries of Schrödinger's equation are obtained in this way: - A free particle corresponds to zero potential energy.
Wave–particle duality
| Property/effect | Equation |
|---|---|
| Planck–Einstein equation | 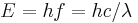
|
| de Broglie wavelength | 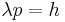
|
| Heisenberg's uncertainty principle | 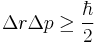
|
Special relativity
Fundamental invariance and unification of space-time and energy-mass-momentum are given below.[5] Both 4-vectors are very analogous, leading to analogous expressions using only the 4-vector dot product. The relativistic analogue to the classical Galilean transformation is the Lorentz transformation.
Lorentz frame tranforms
Let V = any 4-vector.
A boost B(v) in any arbitrary direction at velocity v = (vx, vy, vz), or equivalently β = (βx, βy, βz), without rotation, is given by:
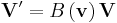
where
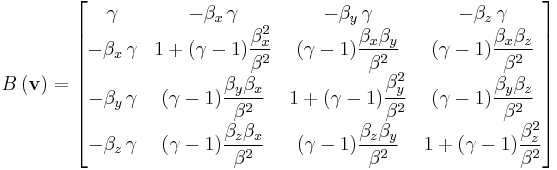
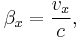
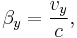
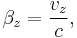
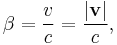 , and
, and 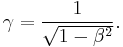
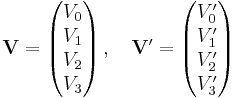
4-vectors and frame-invariant results
| Property/effect | 3-vectors | 4-vectors | Invariant result |
|---|---|---|---|
| Time and proper time | 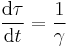 |
||
| Space-time | 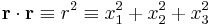 |
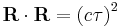
|
|
| τ = Proper time χ = Proper length |
|||
| Velocity transform | 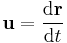 |
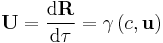 |
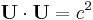 |
| 3-Velocity: u = (u1, u2, u3) 4-Velocity: U = (u0, u1, u2, u3) |
|||
| Momentum-energy invariance |
|
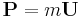 |
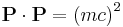
which leads to: |
| E = total energy m = invariant mass |
|||
| Acceleration transform | 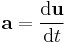 |
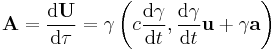 |
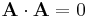 |
| 3-Acceleration: a = (a1, a2, a3) 4-Acceleration: A = (a0, a1, a2, a3) |
|||
| Force transform | 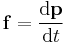 |
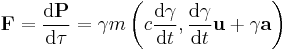 |
 |
| 3-Acceleration: f = (f1, f2, f3) 4-Acceleration: F = (f0, f1, f2, f3) |
Particle Physics
| Name | Equations |
|---|---|
| Strong force | 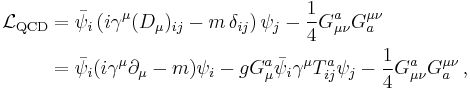 |
| Electroweak interaction | :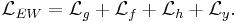
|
| Quantum electrodynamics | 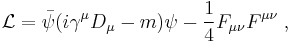 |
See also
References
- ^ Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC Publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1 (VHC Inc.) 0-89573-752-3
- ^ Classical Mechanics, T.W.B. Kibble, European Physics Series, McGraw-Hill (UK), 1973, ISBN 07-084018-0
- ^ Gravitation and Inertia, I. Ciufolini and J.A. Wheeler, Princeton Physics Series, 1995, ISBN 0-691-03323-4
- ^ 2.^ Classical Mechanics, T.W.B. Kibble, European Physics Series, McGraw-Hill (UK), 1973, ISBN 07-084018-0
- ^ Dynamics and Relativity, J.R. Forshaw, A.G. Smith, Manchester Physics Series, John Wiley & Sons, 2009, ISBN 9-780470-014608
 = unit normal to A,
= unit normal to A, = unit vector in direction of J,
= unit vector in direction of J,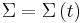 ,
,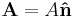
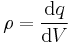 ,
,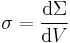 ,
,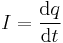
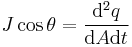 or vector
or vector 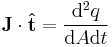
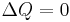
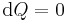
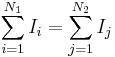
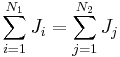
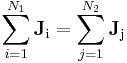
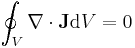
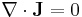
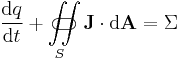
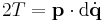
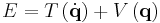
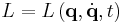
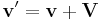
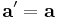
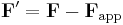
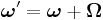
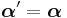
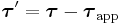
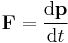
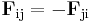
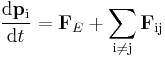
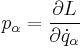
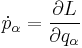
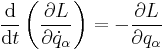
![H = \left [ \mathbf{q}(t), \mathbf{p}(t), t \right ]](/2012-wikipedia_en_all_nopic_01_2012/I/3cb53262000d3aed9c19264d32d2b82b.png)
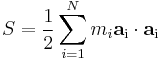
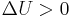 , decrease
, decrease 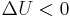
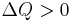 , from system
, from system 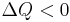
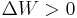 by system
by system 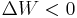
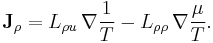
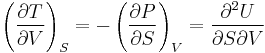
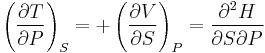
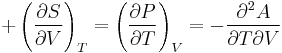
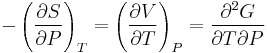
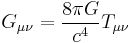
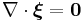
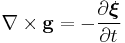
![\nabla \times \boldsymbol{\xi} = \frac{1}{c^2} \left [ -4 \pi G\mathbf{j}_\mathrm{m} %2B \frac{\partial \mathbf{g}} {\partial t} \right ] \,\!](/2012-wikipedia_en_all_nopic_01_2012/I/d3e2e300f9c90c8d689994f05d67ae9d.png)
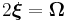
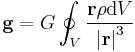
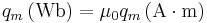
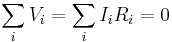
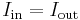
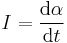
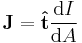
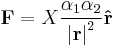
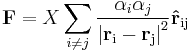
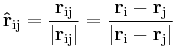
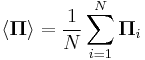
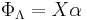
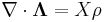
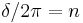
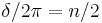
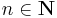
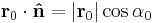
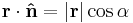
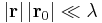
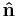 = unit normal vector to the aperture
= unit normal vector to the aperture